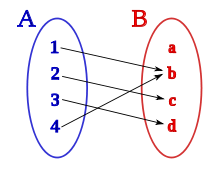
Diagramme représentatif d'une application entre deux ensembles.
En mathématiques, une application est une relation entre deux ensembles pour laquelle chaque élément du premier (appelé ensemble de départ ou source) est relié à un unique élément du second (l’ensemble d'arrivée ou but). Le terme est concurrencé par celui de fonction, bien que celui-ci désigne parfois plus spécifiquement les applications dont le but est un ensemble de nombres ou, encore, englobe plus largement les relations pour lesquelles chaque élément de l'ensemble de départ est relié à au plus un élément de l'ensemble d'arrivée.
Une application est donc un objet issu de la théorie des ensembles, défini par son graphe et associé aux notions d'image et d'antécédent. Elle peut être injective ou surjective selon l'unicité ou l'existence d'un antécédent pour chaque élément de l'ensemble d'arrivée. Une application possédant ces deux propriétés est une bijection, qui admet alors une application réciproque. Les applications peuvent aussi être composées ou restreintes à un sous-ensemble de leur ensemble de départ.
En dehors du contexte de l'analyse, le terme est spécifié entre autres en géométrie affine, en algèbre linéaire, en topologie et dans la théorie des systèmes dynamiques. Il est parfois remplacé par celui d'opérateur ou de morphisme, voire de flèche, notamment en théorie des catégories.
Fonction et application
La notion de fonction en tant que correspondance entre deux types d'objet est relativement ancienne. Mais le terme n'apparait qu'à la fin du XVII siècle sous la plume de Leibniz en 1694, il s'agit alors de fonction associée à une courbe géométrique : Leibniz dit ainsi que l'abscisse, l'ordonnée ou le rayon de courbure d'une courbe en un point M est une fonction du point M. Dans la même époque, Newton parle de fluente pour des quantités dépendant d'une variable qu'il appelle le temps (tout en précisant que le rôle joué par le temps, peut l'être par une autre quantité). La notation sous la forme f ne s'est pas mise en place tout de suite. Jean Bernoulli propose d'appeler X la fonction de x, Leibniz invente une notation permettant de travailler sur plusieurs fonctions différentes : et sont ainsi deux fonctions dépendant de x. La notation fx apparaît chez Euler en 1734. Les fonctions sont alors toujours à valeurs numériques (réelles ou complexes) et possèdent en outre des propriétés restrictives (liées à une équation algébrique, continuité eulérienne, développable en série entière...).
Parallèlement se développe, en géométrie, la notion d'application pour des correspondances ponctuelles.
Dans les années 1950, l'école Bourbaki tente de faire correspondre les deux notions en parlant de :
relation fonctionnelle : (E, F, G) où E et F sont deux ensembles et où G est un sous-ensemble de E × F, appelé le graphe (fonctionnel) de la relation, vérifiant en outre, pour tous couples (x, y) et (x’,y’) de G, si x = x’ alors y = y’ (i.e. chaque élément de E possède au plus une image) ;
application pour une relation fonctionnelle dans laquelle chaque élément de E possède exactement une image.
S'appuyant sur cet avis, les mathématiques modernes des années 1960-70 distinguent alors deux objets différents :
la fonction définie par un ensemble de départ E, un ensemble d'arrivée F et une relation de E vers F dans laquelle chaque élément de E possède au plus une image ; l'ensemble des éléments de E possédant une image est alors appelé domaine de définition de la fonction ;
l'application définie par un ensemble de départ E, un ensemble d'arrivée F et une relation de E vers F dans laquelle chaque élément de E possède une image et une seule (une application est donc une fonction dont le domaine de définition est égal à l’ensemble de départ).
En pratique, le fait qu'il suffise de réduire l'ensemble de départ d'une fonction à son ensemble de définition pour la transformer en application rend peu utile ce distinguo. Celui-ci n'a d'ailleurs jamais été adopté par la communauté mathématique dans son ensemble, pas même durant les années 1960-70. Aujourd'hui, le terme fonction est souvent utilisé comme synonyme du terme application dans le cas particulier où l'ensemble d'arrivée est ℝ ou ℂ (l'ensemble de départ étant alors pris égal au domaine de définition).
Définition
La définition usuelle en mathématiques d'une fonction est donc ensembliste et présuppose essentiellement celle de couple et de produit cartésien. Une application ou fonction est un triplet f = (E, F, G) avec une relation binaire G ⊂ E × F, et qui vérifie que pour tout x de E il existe un unique y de F tel que le couple (x, y) appartienne à G. Exactement dans ce cas, une application fG donnée comme relation binaire G ⊂ E × F est dite bien définie. L'ordre des ensembles du triplet est arbitraire et on trouve d'ailleurs des variations suivant les ouvrages. La propriété caractéristique peut se décomposer en deux clauses :
-
Existence. ∀ x ∈ E ∃ y ∈ F (x, y) ∈ G ;
-
Unicité. ∀ x ∈ E ∀ y ∈ F ∀ y’ ∈ F ( [ (x, y) ∈ G et (x, y’) ∈ G] ⇒ y = y’ ).
En d'autres termes ceci signifie que G intersecte chaque sous-ensemble {x} × F, en un unique point, dont l'existence est donnée par la première clause, et l'unicité par la seconde. Ce point, élément de F, est appelé image de x par l'application f et noté f(x). Pour bien distinguer l'image d'un élément de E, qui est un élément de F, de l'image de f, qui est un sous-ensemble de F, on parle parfois dans ce dernier cas d’ensemble image de f.
On dit également que f associe à x l'élément f(x), ou encore que f envoie x sur f(x). Les formes passives « x est envoyé par f sur f(x) », « f(x) est associé à x par f » sont aussi utilisées.
Si x, élément de E, vérifie f(x) = y, on dit que x est un antécédent de y. Un élément y de F peut très bien avoir plusieurs antécédents ou n'en avoir aucun.
Pour une fonction de E dans F qui à x associe f(x) on note :
-
![f : \begin{array}[t]{lcl}E &\rightarrow & F \\
x & \mapsto & f(x)
\end{array}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/666b0df358343c4f2b124cc03d37e405.png)
par exemple pour la fonction de la variable réelle qui à un nombre associe son carré :
-
![f : \begin{array}[t]{lcl}\Bbb R &\rightarrow & \Bbb R \\
x & \mapsto & x^2
\end{array}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/27b86b5738885a9e017d92b12d6c5453.png)
Dans l'exemple précédent on a utilisé la structure des réels pour définir la fonction. Pour un ensemble E quelconque on peut toujours définir l’identité ou application identique, qui associe à tout élément x de E l'élément x lui-même. Son graphe est la diagonale du produit cartésien E × E, le sous-ensemble défini par la relation x = y.
Si F est non vide, alors on peut associer à tout élément b de F, une application dite application constante de E dans F, qui associe à tout élément de E l'élément b. Son graphe est donc E × {b}.
On utilise parfois d'autres terminologies et d'autres notations. Les fonctions définies sur l'ensemble N des entiers naturels (ou une partie de celui-ci) sont souvent appelées suites, par exemple les suites réelles sont les fonctions de N dans l'ensemble R des réels. On utilise alors la notation indicielle : (un)n ∈ N désigne la suite, écriture qui peut être abrégée en (un), et un désigne l'image par cette suite de l'entier n.
Cette notation s'étend aux familles, indexées par I d'éléments d'un ensemble F donné, qui sont, avec une autre notation et une autre terminologie, des fonctions de I dans F.
Ensemble des applications entre deux ensembles
L'ensemble des applications de E dans F est souvent noté F. Son cardinal ne dépend que des cardinaux respectifs de E et F : |F| = |F|.
Opérations sur les applications
Restriction : soit f une application de E dans F, et soit E’ un sous-ensemble de E. La restriction de f à E’, notée , est l'application de E’ dans F qui à tout élément e de E’ associe l'élément f(e) de F. Autrement dit, si on nomme G le graphe de f, est l'application de E’ dans F de graphe G ∩ (E’ × F).
Corestriction : la corestriction est l'opération analogue sur un sous-ensemble de l'ensemble d'arrivée, mais si on veut que celle-ci reste une application, on ne peut restreindre l'ensemble d'arrivée F de f qu'à un sous-ensemble F’ de F contenant l'ensemble image de f. On obtient alors une application qui a même ensemble de départ et même graphe, mais pas même ensemble d'arrivée.
Prolongement : soient deux applications f de E dans F de graphe G, et f’ de E’ dans F’ de graphe G’. On dit que f’ est un prolongement de f quand :E ⊂ E’ et F ⊂ F’ et G ⊂ G’.(Pour un cas particulier en mathématiques élémentaires, voir Ensemble de définition#Prolongement.)
Composition : la composition de deux applications f de dans et g de dans se note . C'est une application de dans définie, pour tout élément x de , par :Si le graphe de f est et le graphe de g est , le graphe de est :
Injectivité et surjectivité
Une application f de E dans F est dite injective, ou encore est une injection, lorsque tout élément de l'ensemble d'arrivée de f a au plus un antécédent dans l'ensemble de départ par f, ce qui peut s'écrire :
. ou encore par contraposée : .
-
La composée de deux injections est une injection et, inversement, si pour une certaine fonction
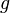 ,
,
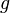 o
o
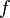 est une injection, alors
est une injection, alors
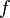 est une injection.
est une injection.
Une application de dans est dite surjective, ou encore est une surjection, lorsque tout élément de l'ensemble d'arrivée est image par f d'au moins un élément de l'ensemble de départ, ce qui s'écrit :En d'autres termes, est surjective ssi son ensemble image est l'ensemble d'arrivée tout entier. La composée de deux surjections est une surjection et, inversement, si est une surjection, alors est une surjection.
Une application f est dite bijective, ou encore est une bijection, lorsque cette application est à la fois injective et surjective, c'est-à-dire que tout élément de son ensemble d'arrivée a un antécédent et un seul par f dans l'ensemble de départ. La composée de deux bijections est une bijection mais inversement, si la composée de deux applications est une bijection, on peut seulement en déduire que l'une est une injection et l'autre une surjection.
Application réciproque
Si une application f : E → F est bijective, à tout élément de F est associé un unique antécédent par f dans E, qui existe puisque f est surjective et qui est unique puisque f est injective. Ceci définit donc une application, que l'on appelle application réciproque de f, et qui, dans ce cas, est également une bijection, dite aussi bijection réciproque de f.
On la note 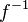 . Son graphe est le symétrique du graphe de f, c'est-à-dire que si G est le graphe de f, le graphe de
. Son graphe est le symétrique du graphe de f, c'est-à-dire que si G est le graphe de f, le graphe de 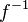 est {(y, x) | (x, y) ∈ G}. Dans le cas où E = F = R, l'ensemble des nombres réels, le graphe de
est {(y, x) | (x, y) ∈ G}. Dans le cas où E = F = R, l'ensemble des nombres réels, le graphe de 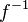 est, dans le plan R², le symétrique de celui de f par rapport à la première bissectrice. Ainsi la fonction des réels positifs dans eux-mêmes qui à x associe x² est une bijection, sa réciproque est la racine carrée, et un graphe de l'une se déduit d l'autre par symétrie par rapport à la droite d'équation y=x.
est, dans le plan R², le symétrique de celui de f par rapport à la première bissectrice. Ainsi la fonction des réels positifs dans eux-mêmes qui à x associe x² est une bijection, sa réciproque est la racine carrée, et un graphe de l'une se déduit d l'autre par symétrie par rapport à la droite d'équation y=x.
Dans le cas par exemple d'une fonction numérique, quand on peut parler de l'inverse d'un élément a de F, celui-ci peut s'écrire a. Dans ce cas 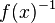 désigne l'inverse de l'élément
désigne l'inverse de l'élément 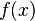 . Il s'agit de la fonction inverse 1/f (si elle existe). La notation
. Il s'agit de la fonction inverse 1/f (si elle existe). La notation 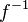 est réservée à la bijection réciproque de f (si elle existe).
est réservée à la bijection réciproque de f (si elle existe).
L'application f : E → F est injective, si et seulement s'il existe une surjection g : F → E réciproque à gauche de f, c'est-à-dire que g ∘ f est l'identité de E. Quand f est injective, il suffit de prendre pour g une application qui à un élément de l'image de f associe son antécédent par f, et qui est définie arbitrairement sur les autres éléments. Cette fonction n'est pas unique, sauf si f est également bijective. La réciproque découle directement de ce que g est une application.
L'application f : E → F est surjective, si et seulement s'il existe une injection g : F → E réciproque à droite de f, c'est-à-dire que f ∘ g est l'identité de F. Supposons f surjective, dans le cas où l'ensemble image de f est infini, l'existence de cette injection repose en toute généralité sur l'axiome du choix (énoncé pour toute surjection, c'est même équivalent à l'axiome du choix). L'application g est en effet une fonction de choix sur l'ensemble des ensembles des antécédents d'un élément de F, elle choisit bien un antécédent pour chaque élément de F. Cette fonction n'est pas unique, sauf si f est également bijective (cas où, l'antécédent étant unique, l'axiome du choix n'est pas nécessaire). L'existence d'une fonction g réciproque à droite de f fournit bien directement un antécédent par f pour chaque élément de F.
Décomposition canonique
On appelle relation binaire associée canoniquement à l'application f la correspondance ℛ définie dans E par :
x est en relation avec y si et seulement si x et y ont une image commune par f.
Cette relation est toujours symétrique et transitive, du fait de l'unicité de l'image, et est également réflexive du fait de son existence, c'est donc une relation d'équivalence.
On peut alors définir l'ensemble quotient E/ℛ et la surjection canonique s correspondante, associée à l'application f. Cette surjection associe à tout élément x de E sa classe d'équivalence par ℛ, qui n'est autre que f({f(x)}), ensemble des antécédents de f(x).
Considérons alors la correspondance i de E/ℛ dans F définie par :
A est en relation avec y si et seulement si A est l'ensemble des antécédents de y par f.
Cette correspondance est une injection, l'injection canonique associée à l'application f. On montre aisément que f = i∘s.
En résumé : Toute application peut être décomposée de façon unique en une surjection et une injection.
Cette décomposition est la décomposition canonique de l'application. Dans cette décomposition :
la surjection s est une bijection si et seulement si f est une injection, c'est-à-dire si f∘f = idE ;
l'injection i est une bijection si et seulement si f est une surjection, c'est-à-dire si f∘f = idF.
Théorie des ensembles
La notion de fonction n'est pas primitive dans les théories des ensembles de Zermelo ou de Zermelo-Fraenkel, et se définit grâce aux notions de couple et de produit cartésien, qui ne sont pas non plus primitives. La notion peut se développer dans la théorie de Zermelo (sans l'axiome de l'infini), avec l'axiome d'extensionnalité, l'axiome de la paire, l'axiome de la réunion, l'axiome de l'ensemble des parties et le schéma d'axiomes de compréhension. On a eu besoin en une occasion, pour montrer en toute généralité l'existence d'une réciproque à droite d'une fonction surjective, de l'axiome du choix.
Il arrive souvent en théorie des ensembles qu'une fonction soit identifiée à ce que l'on a appelé précédemment son graphe. C'est-à-dire qu'une fonction est définie comme un ensemble de couples vérifiant les propriétés d'existence et d'unicité de l'image, dont on vérifie facilement qu'elles ne mettent pas véritablement en jeu les ensembles de départ et d'arrivée : avec cette définition, G est une fonction quand c'est un ensemble de couples vérifiant la propriété d'unicité :
Unicité. ∀ x ∀ y ∀ y’ ( [ (x, y) ∈ G et (x, y’) ∈ G] ⇒ y = y’ ).
L'ensemble de départ de la fonction est l'ensemble des premières projections de G, qui se définit en compréhension, tout comme l'image de la fonction qui est l'ensemble des secondes projections de G (voir l'article produit cartésien pour des détails dépendant de la représentation des couples). Il n'y a plus d'ensemble d'arrivée intrinsèque, c'est-à-dire que f est une fonction de E dans F devient une propriété de f : E est l'ensemble des premières projections de f, et l'ensemble image, ensemble des secondes projections, est inclus dans F. L'injectivité est une propriété qui ne dépend que du graphe de la fonction. Par contre, dans ce contexte, la surjectivité ou la bijectivité deviennent une propriété de f et de l'ensemble d'arrivée choisi (f est surjective de E dans F).
On peut avoir à s'intéresser aux classes fonctionnelles, qui sont des classes de couples vérifiant les deux propriétés indiquées en début de paragraphe, mais portant sur une classe au lieu de l'ensemble G. Le schéma d'axiomes de remplacement, qui complète la théorie des ensembles de Zermelo pour donner celle de Zermelo-Fraenkel, énonce que l'image d'un ensemble par une classe fonctionnelle, est un ensemble, et donc cette classe fonctionnelle est une fonction (comme ensemble de couples).

 词典释义:
词典释义:
 )延
)延 , 延伸;延
, 延伸;延 部分, 延伸部分
部分, 延伸部分 , 突起
, 突起 后果
后果

 上
上 道路
道路 延伸
延伸 ,加
,加 ,拉
,拉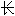 ;
;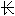 ; 延拓
; 延拓
![f : \begin{array}[t]{lcl}E &\rightarrow & F \\
x & \mapsto & f(x)
\end{array}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/666b0df358343c4f2b124cc03d37e405.png)
![f : \begin{array}[t]{lcl}\Bbb R &\rightarrow & \Bbb R \\
x & \mapsto & x^2
\end{array}](https://wiki-gateway.eudic.net/wikipedia_fr/I/m/27b86b5738885a9e017d92b12d6c5453.png)
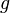 ,
,
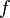 est une injection, alors
est une injection, alors
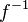 . Son graphe est le symétrique du graphe de f, c'est-à-dire que si G est le graphe de f, le graphe de
. Son graphe est le symétrique du graphe de f, c'est-à-dire que si G est le graphe de f, le graphe de 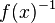 désigne l'inverse de l'élément
désigne l'inverse de l'élément 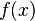 . Il s'agit de la fonction inverse 1/f (si elle existe). La notation
. Il s'agit de la fonction inverse 1/f (si elle existe). La notation