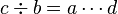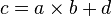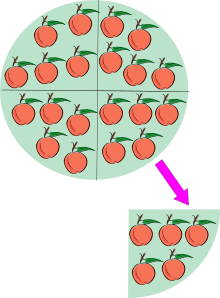
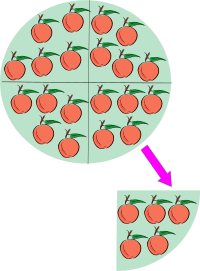
Division en tant que partage. Illustration de 20÷4 : partage d'un ensemble de 20 pommes en 4 parts égales.
La division est une opération mathématique qui à deux nombres a et b associe un troisième nombre (loi de composition interne), appelé quotient ou rapport, et qui peut être noté :
a:b ; a÷b (obèle) ; a/b (barre oblique, fraction en ligne) ; (fraction).
Dans une première approche, on peut voir la quantité a÷b comme une séparation de la quantité a en b parts égales. Mais cette approche est surtout adaptée à la division entre nombre entiers, où la notion de quantité est assez intuitive. On distingue couramment la division « exacte » (celle dont on parle ici) de la division « avec reste » (la division euclidienne).
D'un point de vue pratique, on peut voir la division comme le produit du premier par l'inverse du second. Si un nombre est non nul, la fonction « division par ce nombre » est la réciproque de la fonction « multiplication par ce nombre ». Cela permet de déterminer un certain nombre de propriétés de l'opération.
De manière plus générale, on peut définir le quotient y = a/b comme étant la solution de l'équation
- b×y = a.
Ceci permet d'étendre la définition à d'autres objets mathématiques que les nombres, à tous les éléments d'un anneau.
Problématique
La division sert :
à faire un partage équitable entre un nombre de parts déterminé à l'avance, et donc à déterminer la taille d'une part. Par exemple :
-
Question : Si on répartit équitablement 500 grammes de poudre de perlimpimpin entre huit personnes, combien chacune d'elle obtiendra-t-elle ?
-
Réponse :
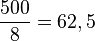 , chacun obtient 62,5 grammes de poudre de perlimpimpin
, chacun obtient 62,5 grammes de poudre de perlimpimpin
à déterminer le nombre de parts possible, d'une taille déterminée à l'avance. Par exemple :
-
Question : Si on répartit 500 grammes de poudre de perlimpimpin par tranche de 70 g, combien de personnes pourra-t-on servir ?
-
Réponse :
 , on pourra servir 7 personnes et il restera de quoi servir 1/7 de personne (≈ 0,14).
, on pourra servir 7 personnes et il restera de quoi servir 1/7 de personne (≈ 0,14).
La multiplication est également l'expression d'une loi proportionnelle. La division permet donc « d'inverser » cette loi. Par exemple, on sait qu'à un endroit donné, le poids P (force qui tire un objet vers le bas, exprimée en newtons) est proportionnelle à la masse m (quantité de matière, exprimée en kilogrammes), le coefficient de proportionnalité étant appelé « gravité » g :
-
P = m×g
Un pèse-personne mesure la force qui lui est exercée, donc P ; la gravité étant connue, on peut en déduire la masse d'une personne en inversant la loi par une division :
- m = P/g.
Dans le même ordre d'idée, dans le cas d'un mouvement rectiligne uniforme, la distance parcourue d (en kilomètres) est proportionnelle au temps t (en heures), le coefficient étant la vitesse moyenne v (en kilomètres par heure) :
- d = v×t.
On peut inverser cette loi pour déterminer le temps qu'il faut pour parcourir une distance donnée à une vitesse moyenne donnée :
- t = d/v.
De manière plus générale, la division intervient dans l'inversion d'une loi affine, c'est-à-dire du type
- y = ax + b
ce qui donne si a est non nul
- x = (y - b)/a
Par ailleurs, on peut approcher la plupart des lois par une loi affine en faisant un développement limité à l'ordre 1. La division permet donc d'inverser une loi de manière approximative : si l'on connaît la valeur de ƒ et de sa dérivée en un point x0, on peut écrire « autour de ce point »
- y = ƒ(x) ≈ ƒ(x0) + ƒ'(x0)×(x - x0)
et ainsi inverser la loi :
-
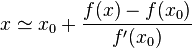
-
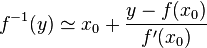
Ceci est par exemple utilisé dans l'algorithme de Newton, qui recherche les zéros d'une fonction :
-
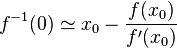
Vocabulaire et notations. Historique
Le symbole actuel de la division est un trait horizontal séparant le numérateur (dividende) du dénominateur (diviseur). Par exemple, a divisé par b se note 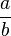 .
.
Le dénominateur donne la dénomination et le numérateur énumère :  indique qu'il s'agit de quarts, et qu'il y en a trois → trois quarts.
indique qu'il s'agit de quarts, et qu'il y en a trois → trois quarts.
Diophante et les Romains, au IV siècle écrivaient déjà des fractions sous une forme semblable, les Indiens également au XII siècle et la notation moderne fut adoptée par les Arabes.
Le symbole « : » a été plus tard utilisé par Leibniz.
Les fabricants de calculatrices impriment l'obèle ÷ ou la barre oblique / sur la touche « opérateur division ». L'utilisation de ces symboles est plus ambiguë que la barre de fraction, puisqu'elle demande de définir des priorités, mais elle est pratique pour l'écriture « en ligne » utilisée en imprimerie ou sur un écran.
Dans les publications scientifiques, on utilise plus volontiers les notations fractionnelles. La notation avec les deux-points est souvent utilisée pour représenter un rapport de quantités entières ou de longueurs.
Aujourd'hui en France, en classe de 6 de collège, les notations ÷, : et / sont utilisées, car la division a pour les élèves un statut d'opération. Une nuance de sens est communément admise :
a ÷ b et a : b désignent une opération (non effectuée), et le vocabulaire approprié est dividende pour a et diviseur pour b ;
et a / b désignent l'écriture fractionnaire du résultat de cette opération, et le vocabulaire approprié est numérateur pour a et dénominateur pour b.
Mathématiques et langue française
On peut diviser une entité en un nombre de parties dont l'addition donne cette entité, par un moyen implicite ou explicite.
Ainsi, on peut :
diviser un gâteau en deux parts, par un coup de couteau
simplement diviser un gâteau en deux [parts, par un moyen quelconque]
diviser 1 en 2 demis, par la représentation mentale mathématique que l'on s'en fait
simplement diviser 1 en 36
etc.
On peut également diviser par dichotomie ou par malice, mais diviser par 2 est un concept mathématique :
-
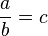 : « a divisé par b est égal à c ».
: « a divisé par b est égal à c ».
Définition
Approche élémentaire
On commence par définir la division « avec reste » entre nombres entiers naturels. Cette division peut s'approcher de manière intuitive par la notion de « partage, distribution équitable », et donne une procédure de calcul.
Cette notion permet déjà de mettre en évidence le problème de la division par zéro : comment partager une quantité en 0 part ? Cela n'a pas de sens, il faut au moins une part.
Puis, on définit la notion de nombre décimal, et l'on étend la procédure de calcul en l'appliquant de manière récursive au reste, voir la section ci-dessous Division non abrégée. Cela permet de définir la notion de nombre rationnel.
La notion de partage convient encore mais est plus difficile à appréhender. On peut imaginer des portions de part, donc diviser par des nombres fractionnaires : diviser une quantité par 0,1 (1/10), c'est dire que la quantité initiale représente 1/10 part, et donc trouver la taille d'une part complète. Diviser une quantité par un nombre négatif, cela revient à calculer la taille d'une part que l'on enlève.
Les nombres réels sont construits à partir des rationnels. Un nombre irrationnel ne peut pas se concevoir comme une quantité ; par contre, il peut se voir comme une proportion : le rapport entre la diagonale d'un carré et son côté, le rapport entre le périmètre d'un cercle et son diamètre. Dès lors, la division ne peut plus être définie comme un partage, mais comme la réciproque de la multiplication.
Avec cette définition, on ne peut toujours pas diviser par 0 : puisque 0×a = 0 pour tout nombre, il existe une infinité de réciproques. On peut aussi — puisque diviser par un nombre revient à multiplier par son inverse — voir ce problème comme celui de la limite en 0 de la fonction inverse ƒ(x) = 1/x : elle a deux limites, –∞ à gauche et +∞ à droite.
Le fait « d'étendre » les nombres réels en incluant des « pseudo-nombres infinis », +∞ et –∞ (droite réelle achevée), ne règle pas le problème, puisque reste le problème du signe.
La notion de division est donc fondamentale en algèbre et en analyse.
Définition complète
Étant donné un anneau intègre (A, +, ×), la division sur A est la loi de composition : , notée par exemple « ÷ », telle que ,
- a ÷ b = c si et seulement si b × c = a.
L'intégrité de l'anneau assure que la division a bien un résultat unique. Par contre, elle n'est définie que sur si et seulement si A est un corps commutatif, et en aucun cas définie pour b = 0.
Si la division n'est pas définie partout, on peut étendre conjointement la division et l'ensemble A : dans le cas commutatif, on définit sur une relation d'équivalence par
-
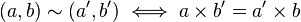
et on écrit
- a ÷ b la classe de
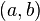 dans l'anneau quotient.
dans l'anneau quotient.
Cet anneau quotien est un corps dont le neutre est la classe 1 ÷ 1. C'est ainsi que l'on construit en symétrisant pour la multiplication (ou à partir de en symétrisant l'addition).
Cette définition ne recouvre pas celle de division euclidienne, qui se pose de manière analogue mais dont le sens est radicalement différent.
Dans l'idée, elle sert aussi à inverser la multiplication (dans a, combien de fois b). Le problème de définition ne se pose plus, puisque 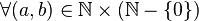 ,
, 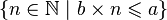 est une partie de
est une partie de 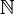 non vide et majorée, qui admet donc un plus grand élément.
non vide et majorée, qui admet donc un plus grand élément.
Cette division, fondamentale en arithmétique, introduit la notion de reste. Néanmoins, comme pour toutes les divisions, le b de la définition ne peut être zéro.
Propriétés
La division n'était pas à proprement parler une opération (loi de composition interne, définie partout), ses « propriétés » n'ont pas d'implications structurelles sur les ensembles de nombres, et doivent être comprises comme des propriétés des nombres en écriture fractionnaire.
Non-propriétés
non commutative car
non associative car
Remarques
pseudo-élément neutre à droite : 1
pseudo-élément absorbant à gauche : 0
égalité de fractions de même dénominateur en général (qui découle de la construction de )
de même dénominateur
en général (qui découle de la construction de )
ordre et sont dans le même ordre que a et c
Algorithmes de la division de nombres décimaux
Division non abrégée
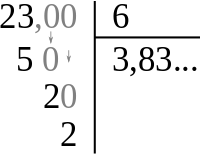
Division non abrégée de 23 par 6.
L'algorithme de division non abrégée, encore appelé division longue, sert à déterminer une écriture décimale du quotient de deux nombres entiers. C'est une extension de la division euclidienne (voir Poser une division > Généralisation en arithmétique). D'un point de vue pratique, il consiste à continuer la procédure, en « descendant des zéros », les nouveaux chiffres calculés s'ajoutant après la virgule. Cela se justifie par
-
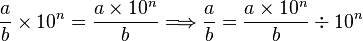
où n est le nombre de décimales que l'on veut. Ainsi, on ajoute n zéros à droite du numérateur, on effectue une division euclidienne classique, puis sur le quotient obtenu, les n derniers chiffres sont après la virgule.
Notons que l'on a intérêt à calculer la n + 1 décimale pour savoir dans quel sens faire l'arrondi.
Par exemple, pour calculer 23÷6 avec deux décimales, la procédure revient à calculer 2 300÷6 ( = 383, reste 2) puis à diviser le résultat par 100 (ce qui donne 3,83).
Cette procédure se généralise au quotient de deux nombres décimaux ; cela se justifie par :
-
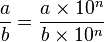
où n est un entier positif tel que a×10 et b×10 soient des entiers ; on peut par exemple prendre le plus grand nombre de décimales dans les nombres a et b.
Deux situations peuvent se présenter :
on finit par avoir un reste nul : on obtient donc un nombre décimal ;
on finit par retomber par un reste qui est déjà apparu auparavant : la division « ne se termine pas », elle boucle à l'infini ; dans ce cas, le quotient est un rationnel non décimal, et on peut prouver que son développement décimal admet une période, dont la longueur est strictement inférieure au diviseur.
Dans une division non exacte a÷b, (a et b étant deux nombres entiers, b non nul), si on note 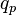 et
et 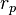 respectivement le quotient et le reste obtenus en poussant les itérations jusqu'à obtenir p chiffres après la virgule du quotient, on obtient un encadrement ou une égalité :
respectivement le quotient et le reste obtenus en poussant les itérations jusqu'à obtenir p chiffres après la virgule du quotient, on obtient un encadrement ou une égalité :
-
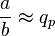 à
à
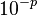 près ou
près ou
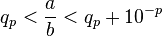
et
-
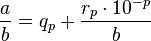
Un nombre irrationnel (réel, sans être rationnel) ne peut s'écrire sous forme de fraction, par définition. C'est par contre la limite d'une suite de nombres rationnels (voir Construction des nombres réels).
Division de nombres codés en binaire
La division en système binaire est une opération fondamentale pour l'informatique.
Division euclidienne binaire
On considère dans un premier temps des entiers naturels (positifs). La division se fait de la même manière que la division euclidienne.
Soient deux nombres a et b de n bits. La notation a(i) désigne le i-ième bit (en partant de la droite, notés de 0 à n - 1), a(i:j) désigne les bits situés entre les positions i et j. La fonction suivante calcule le quotient Q et le reste R, en pseudo-code :
fonction [Q, R] = diviser(a, b)
si b == 0 alors
génère l'exception "division par zéro" ;
fin
Q := 0 ; R := a ; // initialisation
pour i = n-1 → 0
si a(n:i) >= b alors
Q(i) = 1 ; // i-ème bit du quotient
R = a(n:i) - b ; // reste
fin
fin
retourne [Q, R] ;
fin
On cherche une portion de « bits forts » (chiffres de gauche) de a qui est supérieure à b ; si l'on n'en trouve pas, alors le quotient garde la valeur 0, et le reste R prend la valeur a (puisqu'au final il est constitué de tous les chiffres de a). Si à un certain rang i on a a(n:i) ≥ b, alors du fait du système binaire, la réponse à
-
en a(n:i) combien de fois b
est nécessairement « une fois » : en base 10, la réponse est entre 1 et 9 = 10 - 1 ; ici, elle est entre 1 et 1 = 2 - 1. On a donc le i-ème bit du quotient qui vaut 1 ; le reste R à cette étape est la différence.
Ce pseudo-programme n'est pas optimisé pour des raisons de clarté ; une version plus efficace serait :
fonction [Q, R] = diviser(a, b)
si b == 0 alors
génère l'exception "division par zéro" ;
fin
Q := 0 ; R := 0 ; // initialisation
pour i = n-1 → 0
R = décalage_à_gauche_de_bits(R, 1) ; // équivaut à rajouter un 0 à droite
R(1) = a(i) ; // le bit de poids faible de R est le i-ème bit du numérateur
si R >= b alors
Q(i) = 1 ; // i-ème bit du quotient
R = R - b ; // reste
fin
fin
retourne [Q, R] ;
fin
Cet algorithme marche également avec les nombres décimaux codés en virgule fixe.
Pour les nombres décimaux codés en virgule flottante, il suffit de voir que :
-
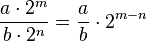
donc on fait la division des mantisses (qui sont des décimaux codés en virgule fixe) d'un côté, et la différence des exposant (qui sont des entiers).
On voit que l'on ne fait appel qu'à des fonctions élémentaires — comparaison, décalage, assignation, soustraction — ce qui permet de le mettre en œuvre de manière simple dans un microprocesseur.
Méthodes lentes
Dans la division euclidienne de a par b, pour des nombres représentés en base B (B = 2 en binaire), à l'étape i :
on considère le reste de l'étape précédente, Ri - 1 ;
on détermine le i-ème chiffre du quotient en partant de la gauche, donc le chiffre j = n - i en partant de la droite : Qn - i ;
le nouveau reste vaut
-
Ri = B×Ri - 1 - Qn - i×b.
Cette construction par récurrence constitue la base des méthodes dites lentes.
Connaissant Ri - 1, on suppose que Qn - i = 1, on a alors
-
Ri = 2×Ri - 1 - b.
Si la valeur trouvée est négative, c'est que Qn - i = 0. Par rapport à la procédure euclidienne, plutôt que de prendre les chiffres de gauche du numérateur, on ajout des 0 à droite du dénominateur. À la première étape, on en ajoute autant que le nombre de bits n servant à coder les nombres (il faut donc un espace mémoire double), puis on multiplie le numérateur par 2 jusqu'à vérifier la condition. Cela donne en pseudo-code (on omet le test de division par zéro) :
fonction [Q, R] = diviser(a, b)
R := a // valeur initiale du reste
b := décalage_à_gauche_de_bits(b, n)
pour i = n-1 → 0
R := décalage_à_gauche_de_bits(b, 1)
si R >= b alors
Q(i) := 1 // le i-ème bit de i est 1
R = R - b
sinon
Q(i) := 0 // le i-ème bit de i est 0
fin
fin
fin
Lorsque l'on optimise l'algorithme pour réduire le nombre d'opérations, on obtient le pseudo-code suivant.
fonction [Q, R] = diviser(a, b)
R := a // valeur initiale du reste
b := décalage_à_gauche_de_bits(b, n)
pour i = n-1 → 0
R := 2*R - b // le reste décalé est-il supérieur à b ?
si R >= 0 alors
Q(i) := 1 // le i-ème bit de i est 1
sinon
Q(i) := 0 // le i-ème bit de i est 0
R := R + b // on restaure la valeur du reste en gardant le décalage
fin
fin
retourner[Q, R]
fin
Du fait de la dernière instruction de la boucle, on qualifie cette méthode de « division avec restauration ».
La méthode peut être améliorée en générant un quotient utilisant les nombres +1 et -1. Par exemple, le nombre codé par les bits
-
11101010
correspond en fait au nombre
-
11111111
c'est-à- dire à
11101010
-00010101
---------
11010101
La méthode est dite « sans restauration » et son pseudo-code est :
fonction [Q, R] = diviser(a, b)
R[0] := a
i := 0
tant que i < n
si R[i] >= 0 alors
Q[n-(i+1)] := 1
R[i+1] := 2*R[i] - b
sinon
Q[n-(i+1)] := -1
R[i+1] := 2*R[i] + b
fin
i := i + 1
fin
Q = transforme(Q)
retourner[Q, R]
fin
La méthode de division SRT — du nom de ses inventeurs, Sweeney, Robertson, et Tocher —, est une méthode sans restauration, mais la détermination des bits du quotient se fait en utilisant une table de correspondance ayant pour entrées a et b. C'est un algorithme utilisé dans de nombreux microprocesseurs. Alors que la méthode sans restauration classique ne permet de générer qu'un bit par cycle d'horloge, la méthode SRT permet de générer deux bits par cycle.
L'erreur de division du Pentium était due à une erreur dans l'établissement de la table de correspondance.
Méthodes rapides
Les méthodes rapides consistent à évaluer x = 1/b, puis à calculer Q = a×x.
La méthode de Newton-Raphson consiste à déterminer 1/b par la méthode de Newton.
La méthode de Newton permet de trouver le zéro d'une fonction en connaissant sa valeur et la valeur de sa dérivée en chaque point. Il faut donc trouver une fonction ƒb(x) qui vérifie
-

et telle que l'on puisse effectuer l'itération
-
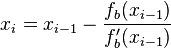
sans avoir à connaître 1/b. On peut par exemple utiliser
-
ƒb(x) = 1/x - b
ce qui donne
- xi = xi - 1(2 - b·xi - 1)
Pour des raisons d'économie de calcul, il vaut toutefois mieux utiliser l'écriture
- xi = xi - 1 + xi - 1(1 - b·xi - 1)
Pour initialiser la procédure, il faut trouver une approximation de 1/b. Pour cela, on normalise a et b par des décalages de bits afin d'avoir b compris dans [0,5 ; 1]. On peut ensuite prendre une valeur arbitraire dans cet intervalle — par exemple b ≈ 0,75 donc 1/b ≈ 1,33…, ou encore 1 ≤ 1/b ≤ 2 donc 1/b ≈ 1,5 —, ou bien faire le développement limité de 1/x en un point — par exemple en 0,75 (1/b ≈ 2,66… - 1,77…×b) ou en 1/1,5 (1/b ≈ 3 - 2,25×b). On retient souvent l'approximation affine
-
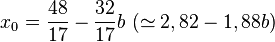
les valeurs de 48/17 et de 32/17 étant précalculées (stockées « en dur »).
Cette méthode converge de manière quadratique. Pour une précision sur p bits, il faut donc un nombre d'étapes s :
-
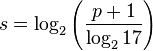
(arrondi au supérieur), soit trois étapes pour un codage en simple précision et quatre étapes en double précision et double précision étendue (selon la norme IEEE 754).
Voici le pseudo-code de l'algorithme.
fonction [Q] = diviser(a, b)
e := exposant(b) // b = M*2^e (représentation en virgule flottante)
b' := b/2^{e + 1} // normalisation ; peut se faire par un décalage de e+1 bits à droite
a' := a/2^{e + 1} // 0.5 <= b <= 1 ; a'/b' = a/b
X := 48/17 - 32/17*b' // initialisation de la méthode de Newton
pour i = 1 → s // s précalculé en fonction du nombre p de bits de la mantisse
X := X + X*(1 - b*X)
fin
Q := a'*X
retourne[Q]
fin
La méthode de Goldschmidt est fondée, elle, sur la considération suivante :
-
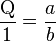
donc, il existe un facteur F tel que b×F = 1, et ainsi a×F = Q. Notons que F = 1/b.
Le facteur F est évalué par une suite (Fk) :
-
Fk = fk×fk - 1×…×f1 = ∏(fi)
telle que la suite (bk) = Fk×b converge vers 1. Pour cela, on normalise la fraction pour que b se trouve dans ]0 ; 1], et l'on définit
- fi + 1 = 2 - bi.
Le quotient final vaut
-
Q = Fk×a.
Notons que l'on a
-
Fi + 1 = fi + 1×Fi ;
- bi + 1 = fi + 1×bi.
Cette méthode est notamment utilisée sur les microprocesseurs AMD Athlon et suivants.
La méthode binomiale est similaire à la méthode de Goldschmidt, mais consiste à prendre pour suite de facteurs fi = 1 + x avec x = 1 - b. En effet, on a :
-
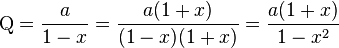
-
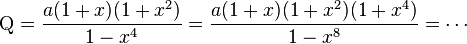
suivant la formule du binôme de Newton.
Si l'on normalise b pour qu'il soit dans [0,5 ; 1], alors x est dans [0 ; 0,5] et à l'étape n, le dénominateur 1 - x est égal à 1 avec une erreur de inférieure à 2, ce qui garantit 2 chiffres significatifs.
Cette méthode est parfois désignée comme « méthode IBM ».
Division d'objets autres que des nombres réels
On peut donc définir la division x = a/b pour tout ensemble muni d'une multiplication, comme étant la solution de l'équation.
- x×b = a
Nous allons voir l'exemple des nombres complexes, des polynômes et des matrices.
Division complexe
Commençons par la notation polaire. Soient deux nombres complexes z1 = r1e, z2 = r2e. La division complexe
- x = z1/z2
est donc définie par
- x×z2 = z1
Si on note x = re, alors l'équation devient
- re×r2e = r1e
soit
- rr2e = r1e
donc
-
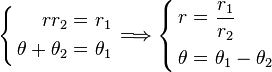
Ceci n'est défini que si r2 ≠ 0 c'est-à-dire z2 ≠ 0
On peut donc écrire
-
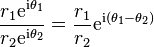
Voyons maintenant la notation cartésienne. On a z1 = a + b×i et z2 = c + d×i, et x = e + f×i. L'équation de définition
- x×z2 = z1
devient
-
(e + f×i)×(c + d×i) = a + b×i
- ec - fd + (de + cf)i = a + b×i
soit
-
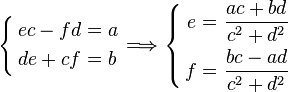
qui est défini si c + d ≠ 0, c'est-à-dire si |z2| ≠ 0, ce qui équivaut à dire que z2 est non-nul.
On peut donc écrire
-
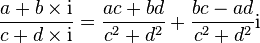
Une mise en informatique « brute » de la méthode de calcul peut mener à des résultats problématiques.
Dans un ordinateur, la précision des nombres est limitée par le mode de représentation. Si l'on utilise la double précision selon la norme IEEE 754, la valeur absolue des nombres est limitée à environ [10 ; 10]. Si le calcul génère une valeur absolue supérieure à 10, le résultat est considéré comme « infini » (Inf, erreur de dépassement) ; et si la valeur absolue est inférieure à 10, le résultat est considéré comme nul (soupassement).
Or, la formule ci-dessus faisant intervenir des produits et des carrés, on peut avoir un intermédiaire de calcul dépassant les capacités de représentation alors que le résultat final (les nombres e et f) peuvent être représentés. Notons que dans la norme IEEE 754, 1/0 donne Inf (+∞) et -1/0 donne -Inf (-∞), mais en mettant un drapeau indiquant l'erreur « division par zéro » ; le calcul de 1/Inf donne 0.
Si par exemple l'on met en œuvre cette formule pour calculer
-
(1 + i)/(1 + 10i), on obtient 0 alors que le résultat est environ 10 - 10i (ce qui est représentable) ;
-
(1 + i)/(10 + 10i), on obtient
NaN (résultat d'une opération 0/0), alors que le résultat est 10 (représentable) ;
Ces erreurs sont dues au calcul de (10) et de (10).
Pour limiter ces erreurs, on peut utiliser la méthode de Smith, qui consiste à factoriser de manière pertinente :
-
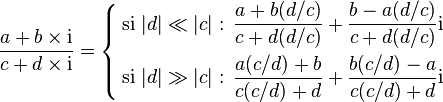
En effet, dans le premier cas, |d/c| < 1 donc |x(d/c)| < x (x = a, b, d), donc la méthode est moins sensible aux dépassements.
Division matricielle
La multiplication matricielle n'étant pas commutative, on définit deux divisions matricielles.
Division à droite
Soit A une matrice de dimension m×n et B une matrice de dimension n×p, alors on appelle « division à droite de A par B » et on note
-
X = A/B
la matrice de dimension m×p vérifiant l'équation :
-
XB = A
Théorème — Si B est une matrice régulière (matrice carrée inversible), alors X = A/B est équivalent à X = AB
Démonstration
Il vient immédiatement de
-
XB = A
que
-
(XB)B = AB
ce qui donne le résultat par associativité.
Division à gauche
Soit A une matrice de dimension m×n et B une matrice de dimension m×p, alors on appelle « division à gauche de A par B » et on note
-
X = A\B
la matrice de dimension n×p vérifiant l'équation :
-
AX = B
Si la matrice A n'est pas de rang maximal, la solution n'est pas unique. La matrice AB, où A désigne la matrice pseudo-inverse, est la solution de norme minimale.
Théorème — Si A est une matrice régulière (matrice carrée inversible), alors X = A\B est équivalent à X = AB
Démonstration
Il vient immédiatement de
-
AX = B
que
-
A(AX) = AB
ce qui donne le résultat par associativité.
On a par ailleurs :
-
B/A = (A\B).
Division de polynômes
On peut défnir la division de polynômes à la manière de la division euclidienne :
-
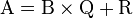
-
deg(R) < deg(B)
où Q et R sont des polynômes ; Q est le quotient et R est le reste.
On peut également appliquer la méthode de construction des nombres rationnels aux polynômes, ce qui permet de définir de manière formelle une fraction de polynômes. Mais il ne s'agit pas là d'un « calcul » de division, il s'agit de définir un nouvel objet mathématique, un nouvel outil.

 词典释义:
词典释义:
 ,
,  开, 划
开, 划 ; 等
; 等 :
: 一块土地
一块土地 成360度
成360度 度机
度机 配给几个工人
配给几个工人 隔
隔 裂, 使不和, 使有
裂, 使不和, 使有 歧:
歧: 们
们 歧的问题所在。
歧的问题所在。  而治之。
而治之。  ,
,  成,
成,  开:
开: 为二”的辨证
为二”的辨证 析方法
析方法 成12个月
成12个月 岔的路
岔的路 裂,
裂, 

 歧
歧 割+er动词后缀
割+er动词后缀
 割
割
 ,
, 开,划
开,划 除,除法
除,除法 开,使
开,使 离;
离; 合,
合, 结;
结; 合,再
合,再 合;
合; 解;
解; ;
; 配;
配; 解,使
解,使 离;
离; 度机
度机
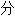 度头
度头
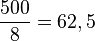 , chacun obtient
, chacun obtient  , on pourra servir 7 personnes et il restera de quoi servir 1/7 de personne (≈ 0,14).
, on pourra servir 7 personnes et il restera de quoi servir 1/7 de personne (≈ 0,14).
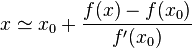
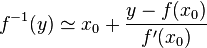
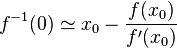
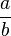 .
. indique qu'il s'agit de quarts, et qu'il y en a trois → trois quarts.
indique qu'il s'agit de quarts, et qu'il y en a trois → trois quarts.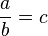
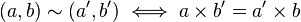
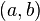 dans l'anneau quotient.
dans l'anneau quotient.
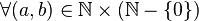 ,
, 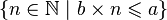 est une partie de
est une partie de  non vide et majorée, qui admet donc un plus grand élément.
non vide et majorée, qui admet donc un plus grand élément.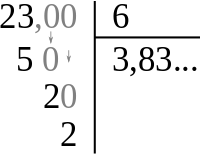
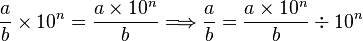
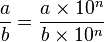
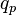 et
et 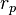 respectivement le quotient et le reste obtenus en poussant les itérations jusqu'à obtenir p chiffres après la virgule du quotient, on obtient un encadrement ou une égalité
respectivement le quotient et le reste obtenus en poussant les itérations jusqu'à obtenir p chiffres après la virgule du quotient, on obtient un encadrement ou une égalité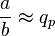 à
à
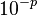 près ou
près ou
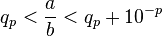
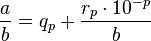
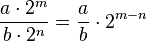

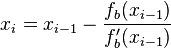
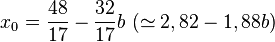
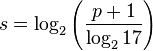
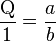
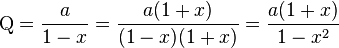
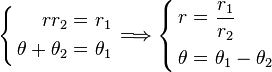
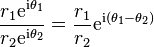
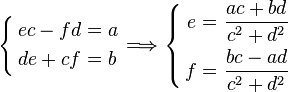
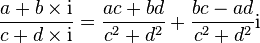
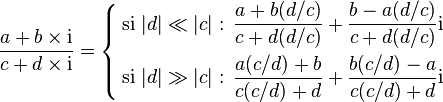
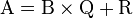
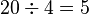
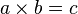
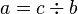 。上面等式中,a 叫做
。上面等式中,a 叫做